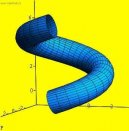
Archimédova serpentina (Odvozeni)
Odvozeni archimédové serpentiny
První způsob:
Šroubovice má tvar: X(v) = [a cos v, a sin v, b v].
Normála ke šroubovici bude mít tvar (jako první derivace souřadnic šroubovice):
T(v) = [- a sin v, a cos v, b]
Vektor hlavní normály křivky bude mít tvar (jako druhá derivace souřadnic šroubovice):
N(v) = [- a cos v, - a sin v, 0]
Vektor binormály k teto křivce (jako vektorový součin T(v) a N(v)):
V(v) = N(v)*T(v) = [ a b sin v, - a b cos v, a2]
Ted´ najdeme jednotkové vektory n, b (vydělíme normou).
n(v) = [- cos v, - sin v, 0]
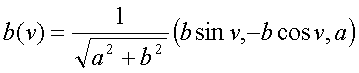
(Vektory n, b, t - tvoří Fremetův repér).
Zůstává nám jen dosadit do vzorce:
X (u,v) = X(v) + R cos (u) n(v) + R sin (u) b(v)
Druhý způsob:
Šroubovice má tvar: X(u) = [a cos u, a sin u, b u], normála ke šroubovici bude mít tvar: n(u) = [-a sin u, a cos u, b] (jako první derivace souřadnic šroubovice).
Zároveň tato normála bude normálou roviny, kde se nachází původní kružnice, která šroubuje. Ted´ hledáme odchylku této roviny, od roviny XY (rovina XY má normálu [0,0,1]
1). Bod A – střed původní kružnice má souřadnice (a, 0, 0). To znamená, že rovnice původní roviny bude mít tvar ay + bz = 0. (Viz. Rovina).
2). Odchylku dvou rovin, spočteme jako odchylku dvou normál podle vzorce:

S toho najdeme:
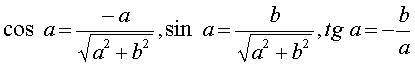
Budeme uvažovat tak, že máme kružnice, která leží v rovině XZ a má souřadnice [r cos u + a, 0, r sin u].
Ted´ potřebujeme najit rovnici původní kružnice:
1). Souřadnice X(u) se nezmění a bude se rovnat [r cos u + a].
2). Souřadnice Y(u) se změní a bude se rovnat [z sin a].
3). Souřadnice Z(u) se nezmění a bude se rovnat [r sin u].
Nebo [r cos (u) + a, - r sin (u) sin(a), r sin (u)].
Vektorový systém šroubovice:
 ,a archimedová serpentina bude mít tvar: Y(u,v) = X(u)e1 + Y(u)e2 + Z(u)e3 nebo
,a archimedová serpentina bude mít tvar: Y(u,v) = X(u)e1 + Y(u)e2 + Z(u)e3 nebo
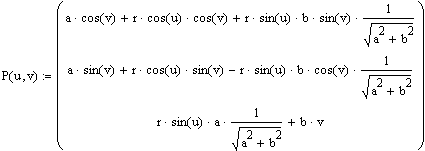
bv – zajistí posun podle osy Z.
| Foto / obrázky k článku Archimédova serpentina |
|
Legální použití článku Text článku je dostupný pro Váš blog/web za podmínek |
| Poradna k článku Archimédova serpentina |
Diskuze k článku Archimédova serpentina |
Fotosoutěž Psi, kočky a td. |
Podpořte nás · Kontakt· Kniha návštěv · RoboStav
Copyright (c) 2026 by CELÝSVĚT. Všechna práva vyhrazena!
Kontaktní e-mail: celysvet(zav)email.cz
|
Fotogalerie (1)...Přidat foto... |
| Poradna | |
 | |
| Poslední dotazy: | |
| 29.10: Máte-li zájem o jakékoli podrob nější informace na téma: Archimédo va serpent... | |
| HELP ! | |
IQ test online
Hry online